Previous Quizzes
Winner of the Quiz
Yeshwant Anandan
Kiewit
Incremental Launch Quiz Series
27 - 03 Dec 2025
Week 3 – LTB-Limited Flexural Capacity
Estimated Time: 4–5 min | PDH/CPD: 0.5 hr | Difficulty: Intermediate
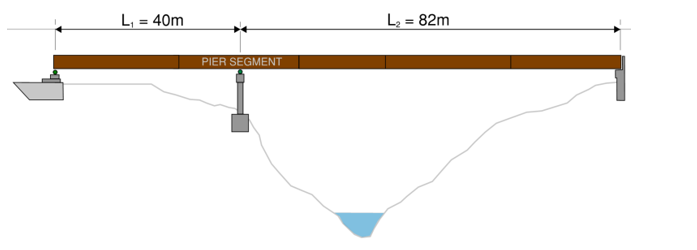
Background: The Sombrio bridge is a two-span composite steel plate girder bridge (40 m + 82 m) launched across a deep ravine in Port Renfrew, BC. Four plate girders were incrementally launched without a temporary pier or launch nose, using precast deck panels as tail counterweight, thickened pier-segment bottom flanges, and crane-assisted final lift. (Parameters simplified for conceptual learning. Allow +25% for cross-frames, connection & splice plates. Girders launched without formwork; ignore wind.)
Engineer's Mind: Quiz 1 ignored lateral-torsional buckling. During launching, the bottom flange at the pier is in compression, unbraced except at cross-frames (8 m spacing). Detailed LTB analysis shows capacity reduces to ~65% of yield strength. Apply CSA S6-19 resistance factor φ = 0.90.
Question: Given that LTB analysis shows capacity reduces to 65% of yield strength, and CSA S6-19 requires resistance factor φ = 0.90 for steel in flexure, what is the factored LTB-limited moment resistance? Given:
• M_y = 52 MN·m (from Quiz 1)
• LTB reduction factor = 0.65
• φ = 0.90 (CSA S6-19 Clause 10.3)
- 26 MN·m
- 34 MN·m
- 30 MN·m
- 47 MN·m
Explanation
Lateral-torsional buckling (LTB) occurs when compression members deflect sideways and twist before yielding. Per CSA S6-19 Clause 10.10.2 LTB resistance depends on: unbraced length, flange slenderness, section torsional properties, and moment gradient. Detailed CHBDC calculations involve lateral slenderness parameters, elastic critical moment, and moment modification factors—beyond this quiz scope.
For this stocky section (700×65 mm flanges, 2750 mm web) with 8 m unbraced length, high level LTB calcs indicate approximately 65% of elastic capacity is achievable. At the pier (negative moment), the bottom flange is always in compression with 8 m cross-frame spacing—unchanged between launch and service. The critical difference: during launching, high cantilever moment is resisted by non-composite steel section.
Note: The 65% LTB reduction factor is based on high-level CSA S6-19 Clause 10.10.2 [JR1] calculations considering section geometry, unbraced length, and loading conditions. Engineers should perform rigorous lateral-torsional buckling analysis for actual design.
Calculation:
- M_n = 0.65 × 52 = 33.8 MN·m (nominal LTB-limited capacity)
- M_r = 0.90 × 33.8 = 30.4 MN·m ≈ 30 MN·m
Learning Resources:
- CSA S6-19 Clause 10.10.2 [JR2] – Resistance Factors
- CSA S6-19 Clause 10.10.2 [JR3] – Lateral-Torsional Buckling
- CISC Handbook of Steel Construction – LTB Design Charts